Project Overview
Building hybrid images and learning about filters
Part 1.1: Finite Difference Operator
Applying the dx and dy filter, followed by gradient magnitude at different thresholds
We have the x and y component of the gradient (that is what the dx and dy filters capture) to find gradient magnitude all we have to do is take the 2 norm at each point.
Gradient magnitude at different thresholds: 0, 5, 15, 30
Applying a gaussian filter (kernel 18, sigma 3)
What differences do you see?
Then taking the x, y and gradient magnitude filters. Notice how the smoothing effects makes the gm much smoother without having to mess with the threshold.
The grass is still a bit blurry but overall it captured all the details in one pass. It did delete some of the information on the hand though.
Doing the same thing with a single convolution instead of two by creating a derivative of gaussian filters.
Part 2.1: Image "Sharpening"
Here is the image being sharpened at alpha = 0, 0.1, 0.5, 1
A picture of my brother, sharpened at alpha = 0, 0.1, 0.5, 1
Here is my brother, first being blurred with a gaussian filter, and then I try to sharpen from scratch. Notice that although it looks better, it does not look like the original, some information can not be recovered. \\
Part 2.2: Hybrid Images
Starting Images.
The hybridization process failed on the left example of "roomate + car".
The high pass filter did not affect the car enough and as a result you can see the car at any distance.
Hybrid images:
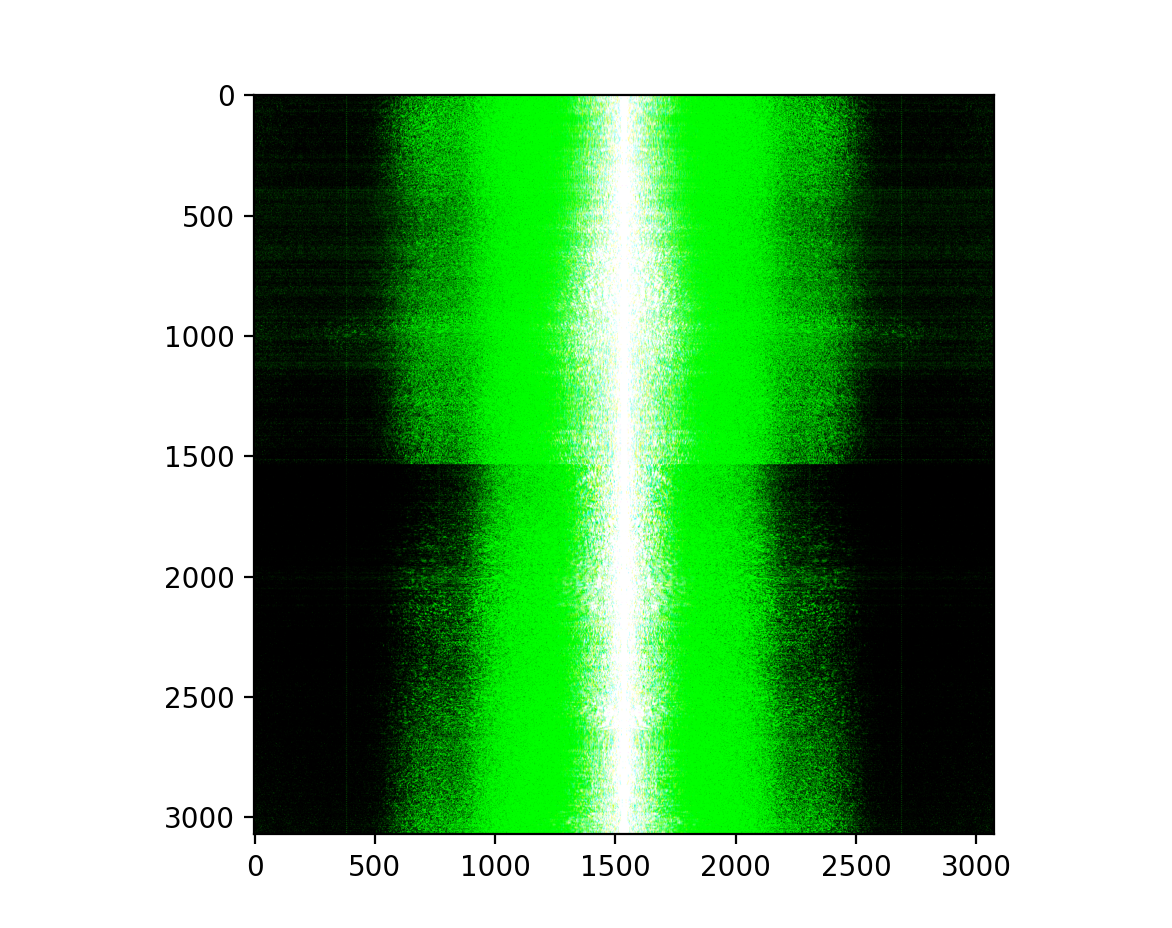
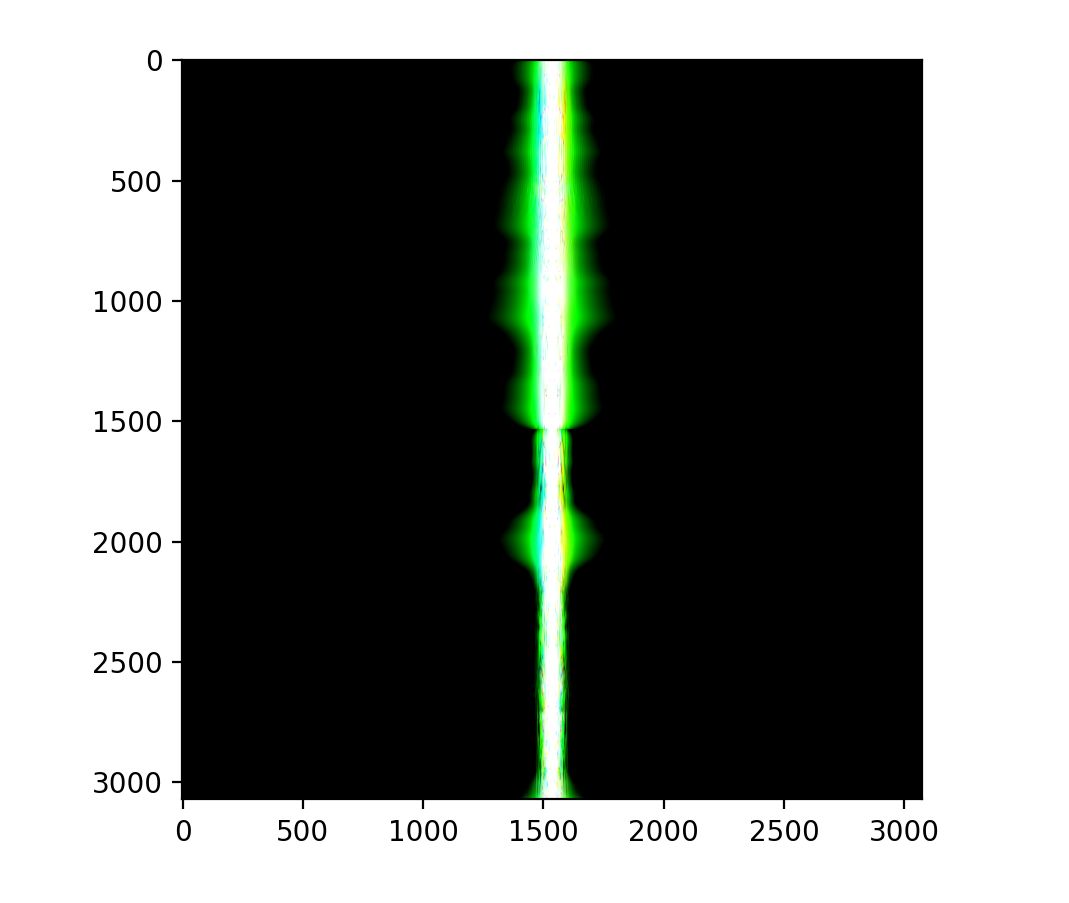
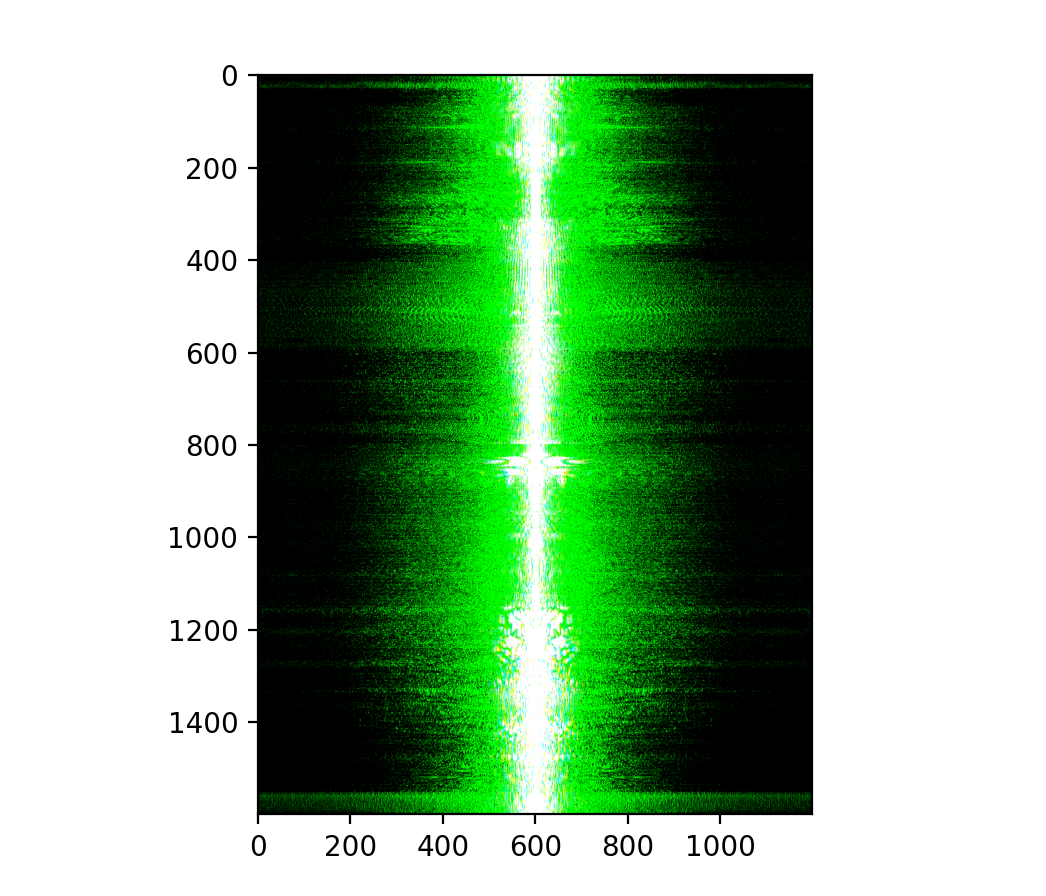
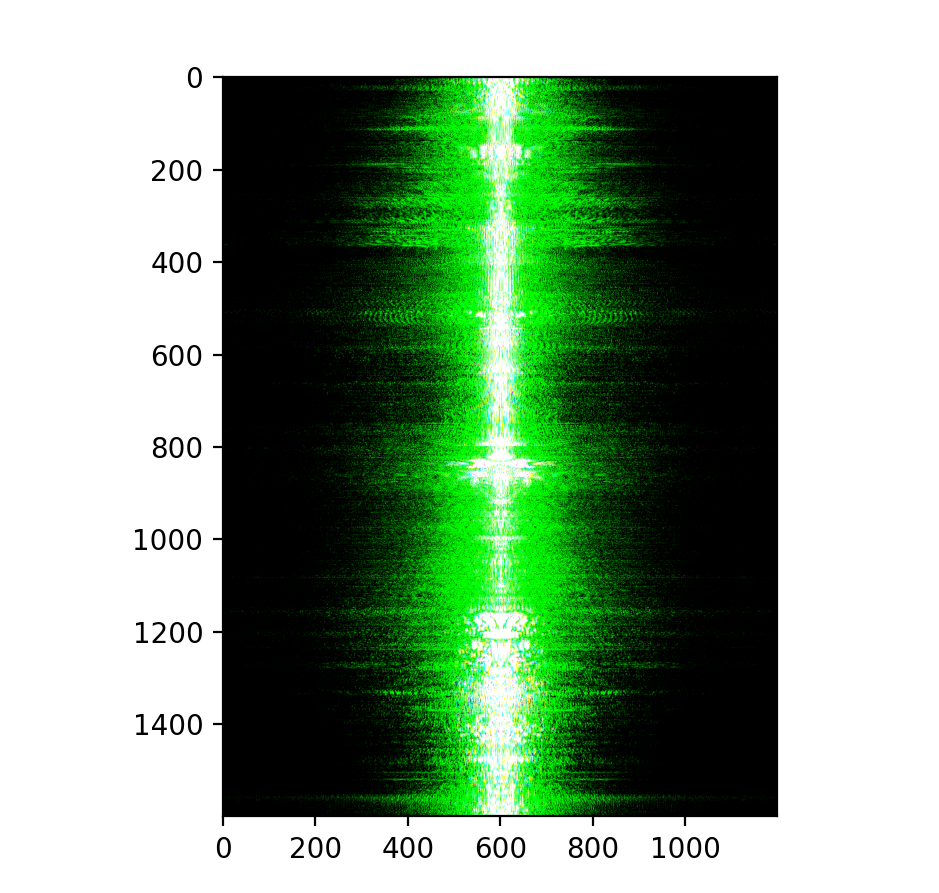
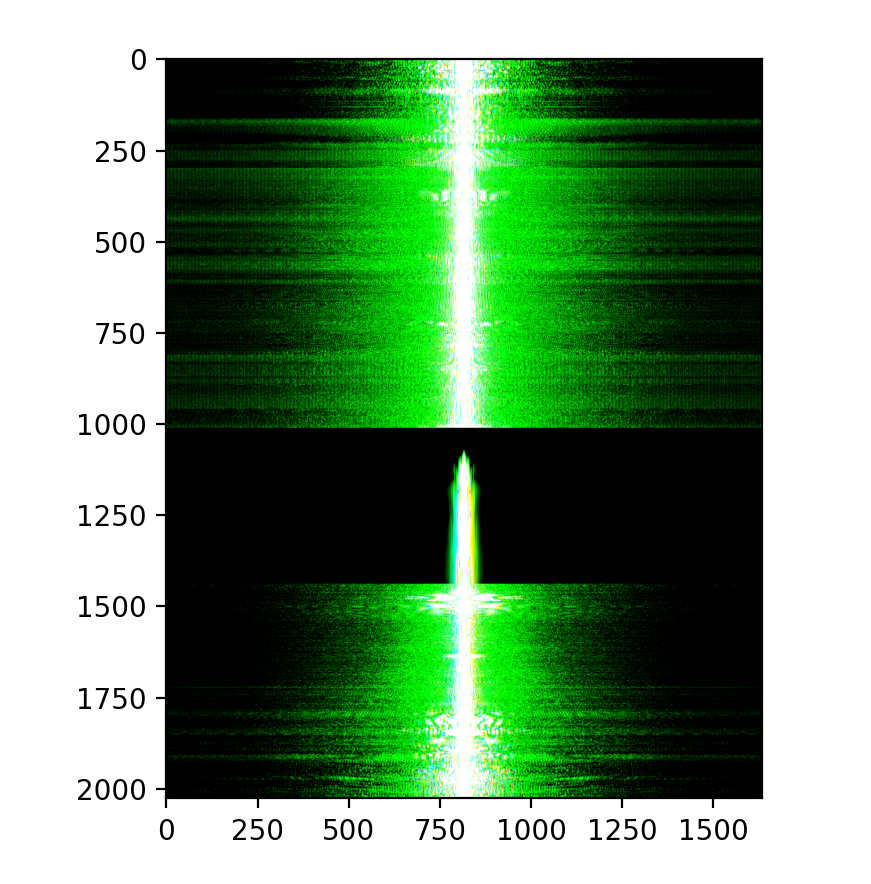
Favorite image signal analysis.
Color makes the low and high frequency component stand out. Compare my Color image to the example solution image.
For the low-pass image, the Fourier transform shows stronger low frequencies with the high frequencies suppressed.
For the high-pass image, the Fourier transform shows the low frequencies removed, showing more prominent high-frequency components.
Hybrid Image: The Fourier transform of the hybrid image shows both low and high-frequency components clearly: the low taken from the low pass image and the high from the high pass image.
Part 2.4: Multiresolution Blending (a.k.a. the oraple!)
A Gaussian stack is a series of progressively blurred versions of an image that capture the “low” frequencies of an image.
A Laplacian stack is a series of images representing high frequencies of an image at different scales,
highlighting details at each scale. It is constructed by subtracting successive levels of a Gaussian pyramid, capturing high-frequency information (edges).
The final layer of the laplacian stack should be the missing low frequencies (last layer in the Gaussian stack).
Collapsing the laplacian stack should return the original image:
Visualising the stacks:
In order to create the oraple we have to create a gaussian stack of the half on half off mask.
Fiannaly to assemble "The Oraple" we simply apply our mask stack to our laplacian stack and collapse the result:
Doing the same thing with all the color channels results in the true Oraple. Some smudges due to normalizing issues.
We don't have to limit ourselves to the left right mask, we can use any mask so long as we follow the same principles. Here is a circle mask alongside other cool merges.
eyeple the apple of my eye
Bells, whistles and all things things
Reflections:
I learned that you can split a 2d gaussian convolution into two 1d gaussian filters. Fast stuff.
I had a lot of trouble normalizing images. If I were to re write my code from the begining I would have made more functions that could handle floating point numbers instead of converting everything to ints
References
The hybrid images part of this assignment is borrowed from Derek Hoiem's Computational Photography class.
Information
This website contains transitions not captured by the pdf, spesificaly, the title image changes into a high gamma verison and then into the black and white threshold filter version.